- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
不止于备课
不止于备课
切换分站
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
从学生的年龄特点和认知水平来看，初二的学生已经具有了较强的逻辑思维能力，能静下来思考几何问题，比较喜欢一些更有深度的严格的推理证明。
多媒体、剪刀、硬纸、三角板
一．知识目标
1.理解三角形中位线的定义；
2.掌握三角形中位线定理证明及其应用，培养学生的转化与化归思想；
3.通过动手操作与合作交流，发展学生的合作交流、实践操作及推理能力。
二．能力目标
1.通过动手操作与合作交流，发展学生的合作交流、实践操作 推理能力。
2.通过对三角形中位线定理的猜想及证明，提高学生分析问题及解决问题的能力。
三．情感态度和价值观目标
鼓励学生大胆猜想，大胆探索新颖独特的证明方法和思路，让学生充分经历“观察、归纳、猜想、推理及应用”这一过程，体会合情推理与演绎推理在获得结论的过程中发挥作用，同时渗透化归思想。
重点：三角形中位线定理及其应用，培养学生的转化与化归思想
难点：利用三角形中位定理证明几何问题，培养学生适当添加辅助线的能力
情景教学与过程学习法、讲授法、小组合作
知识回顾
1.平行四边形的性质；平行四边形的判定；它们之间有什么联系？
2.你能说说平行四边形性质与判定的用途吗？
（答：平行四边形知识的运用包括三个方面：一是直接运用平行四边形的性质去解决某些问题．例如求角的度数，线段的长度，证明角相等或线段相等；二是判定一个四边形是平行四边形，从而判定直线平行等；三是先判定一个四边形是平行四边形，然后再眼再用平行四边形的性质去解决某些问题．）
创设情境
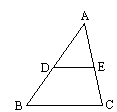
实验（剪纸小游戏）：请同学们思考：将任意一个三角形分成四个全等的三角形，你是如何切割的？（答案如图）
图中有几个平行四边形？你是如何判断的？
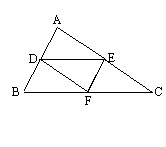
例1 如图，点D、E、分别为△ABC边AB、AC的中点，求证：DE∥BC且DE=1/2BC．
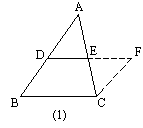
分析：所证明的结论既有平行关系，又有数量关系，联想已学过的知识，可以把要证明的内容转化到一个平行四边形中，利用平行四边形的对边平行且相等的性质来证明结论成立，从而使问题得到解决，这就需要添加适当的辅助线来构造平行四边形．
方法：如图（1），延长DE到F，使EF=DE，连接CF，由△ADE≌△CFE，可得AD∥FC，且AD=FC，因此有BD∥FC，BD=FC，所以四边形BCFD是平行四边形．所以DF∥BC，DF=BC，因为DE=DF，所以DE∥BC且DE=1/2BC．（也可以过点C作CF∥AB交DE的延长线于F点，证明方法与上面大体相同）
1.定义：连接三角形两边中点的线段叫做三角形的中位线．
【思考】：
（1）想一想：①一个三角形的中位线共有几条？②三角形的中位线与中线有什么区别？
（2）三角形的中位线与第三边有怎样的关系？
（答：（1）一个三角形的中位线共有三条；三角形的中位线与中线的区别主要是线段的端点不同．中位线是中点与中点的连线；中线是顶点与对边中点的连线．
（2）三角形的中位线与第三边的关系：三角形的中位线平行与第三边，且等于第三边的一半．）
2.三角形中位线的性质（定理）：三角形的中位线平行于第三边，且等于第三边的一半．
〖拓展〗利用这一定理，你能证明出在设情境中分割出来的四个小三角形全等吗？（让学生口述理由）
例2（补充）已知：如图（1），在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点．
求证：四边形EFGH是平行四边形．
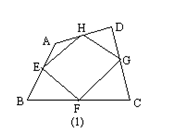
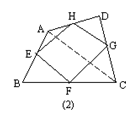
证明：连结AC（图（2）），△DAG中，
∵ AH=HD，CG=GD，
∴ HG∥AC，HG=1/2AC（三角形中位线性质）．
同理EF∥AC，EF=1/2AC．
∴ HG∥EF，且HG=EF．
∴ 四边形EFGH是平行四边形．
此题可得结论：顺次连结四边形四条边的中点，所得的四边形是平行四边形．（如图2所示）
1．如图，A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=20 m，那么A、B两点的距离是 m，理由是 ．
2．已知：三角形的各边分别为8cm 、10cm和12cm ，求连结各边中点所成三角形的周长．
1.布置作业：教材P50,“习题18.1”第5题.
2.完成《学法大视野》中本课时前半部分练习.
1.三角形的中位线具有什么性质？（文字语言和符号语言分别是什么？）
2.三角形的中位线定理怎么去运用？
设为正确答案
