- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间

不止于备课

切换分站

恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



“课题学习 最短路径问题--将军饮马问题”是人教版八年级上册第十三章《轴对称》第4节的内容.在学习本节课之前,学生已经学习过两点之间线段最短、三角形任意两边之和大于第三边、轴对称的性质及作图等知识,为本节课的学习打下了坚实的基础.本堂课探究学习平面内位于直线同侧的两点到直线上的某一点距离之和为最小值时点的位置的确定, 即“将军饮马问题”,能运用轴对称将位于直线同侧的两点转化为位于直线异侧的两点,从而将“将军饮马问题”转化为“两点之间线段最短”问题,并能运用“将军饮马”问题模型解决实际问题.将军饮马问题属于运用几何来探究代数问题,是代数与几何沟通的桥梁,是学生直观感知与领悟数形结合的有效渠道.并且将为今后解决代数与几何综合题中的最值问题奠定基础.
八年级的学生形象直观思维较强,但也有了初步的抽象思维能力,具有一定的独立思考、实践操作、归纳概括等能力,能够进行简单的推理论证.因此,本节课可通过从创造故事情境出发,引导学生经历实践操作、合作交流、类比探究等数学活动,探索解决最短路径问题的方法,体会图形的变换在解决最值问题中的作用,从而渗透培养数学抽象、直观想象、逻辑推理等数学核心素养和转化归纳、数形结合、数学建模、类比探究等数学思想方法.
1.能利用轴对称、两点之间线段最短等知识解决简单的最短路径问题,体会图形的变换在解决最值问题中的作用;
2.在“实际问题-->几何模型-->数学问题”的过程中,提高学生分析问题、解决问题的能力,感受到数学学习的实用性,提高数学学习的兴趣;
3.学生在活动探究、合作交流中提高探究能力和团队精神,培养数学抽象、直观想象、逻辑推理等数学核心素养,渗透转化归纳、数形结合等数学思想方法.
教学重点:
利用轴对称将最短路径问题转化为两点之间线段最短问题。
教学难点:
探索解决最短路径问题的方法.
将军饮马问题
条件特点:“两定一动”、“一定两动”
问题特点:求线段和的最小值
求解思路:利用轴对称,化折为直
求解原理:两点之间,线段最短.(或“三角形任意两边之和大于第三边”)
(一)创设情境
“白日登山望烽火,黄昏饮马傍交河。”,这是唐代诗人李颀《古从军行》里的一句诗。诗句中描述了一位将军每天白天登山观察烽火台的情况,黄昏回军营之前都要带着自己的马去小河边喝水。由此却引申出一系列非常有趣的数学问题——“将军饮马”,今天让我们一起走进这位将军的生活,了解这背后的数学问题。
【导入课题】 最短路径问题--将军饮马问题
(二)明确学习目标
【设计意图】创设情境,动画演示,以趣引题,激发思考,为下一步的探究打好铺垫,做好引导。
(一)自主探究
专题一:创造情境,初识模型
诗句中这位将军每天白天登山观察烽火台的情况,黄昏回军营之前都要带着自己的马去一条笔直的小河边喝水。已知这座山A和军营B分别位于河流l的两岸,请问马儿在哪里喝水,将军回军营的路径最短?(小河的宽度忽略不计)
1.用几何画板构造几何模型:

2.学生解答.
【总结】原理:两点之间,线段最短.(或“三角形任意两边之和大于第三边.”)

【设计意图】通过专题一中直线异侧两点间路径最短的问题,一方面唤醒学生已有的有关最短路径的知识,另一方面为探究同侧两点路径最短(将军饮马问题)做准备。引导学生体会如何将实际问题转化为数学问题,体会数学建模思想。
专题二:动手探究,有效转化
后来这位将军换了一座山观察有无烽火台的警报,已知现在这座山脚点A和军营点B位于河流的同一侧,将军回军营前仍带着马儿去河边喝水,这时马儿在哪喝水,路径最短呢?
1.根据问题描述,画出几何模型:

2.几何画板动态演示,学生观察猜测
几何画板动态演示,明确距离之和在变大变小之间肯定有一个最小值。
学生观察猜测怎么确定当距离之和为最小值时动点的位置。
3.学生小组合作进行类比探究,并展示.
4.明确作法:
(1)作出点A关于直线l成轴对称的点A′。
(2)连接BA′,BA′与直线l相交于点P,则点P即为所求。
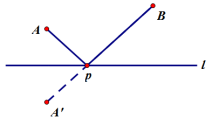
5.规范推理证明
你能用所学的知识证明当A′、P、B三点共线时,PA +PB是最短的吗?
提示:在证明“路径最短”作法的合理性时,常常在直线l上任取一点Q(与所求作的点P不重合),通过与求证的那个 “最小”的量进行比较来证明。由于另取的点具有任意性,所以结论对于直线上的每一点(P点除外)都成立。
证明:在直线l上任取一点Q(点Q不与点P重合),连接QA,QB,QA′.

由轴对称的性质可知,PA′=PA,QA′=QA,
∴PA+PB=PA′+PB,QA+QB=QA′+QB.
∵A′、P、B三点共线
∴PA+PB=PA′+PB=BA′
∵QA′+QB ˃ BA′
∴QA+QB ˃ PA+PB
即当A′、P、B三点共线的时候,PA +PB最短.
【总结】

求一条折线段的长度,可以通过轴对称“化曲为直”,即将动点所在直线同侧的两定点中的一个映射到直线的另一侧,把折线段转化为直线段,将最短路径问题转化为两点之间线段最短问题。
【设计意图】专题二的难点在于PA+PB是一段折线段,通过观察图形很难得出结果,因此采用活动探究,让学生通过画图、观察、与专题一的类比探究发现直线异侧两点的最短路径问题可利用轴对称的知识转化成同侧两点的最短路径问题,将折线段变为直线段。通过搭建台阶,为学生探究问题提供“脚手架”,将“同侧”难于解决的问题转化为“异侧”,渗透转化数学思想。引导学生把握研究问题的基本策略、基本思路和基本方法,体会轴对称在解决问题中的作用,感悟转化思想的重要价值。规范作图、作法,并对结论进行推理证明,提高学生知识运用能力和迁移能力,让学生进一步体会作法的正确性,提高逻辑思维能力。
(二)合作共研
1.生生交流自主探究的情况。
2.学生展示探究结果。
3.学生质疑补充,老师综合点评。
将军奉命守卫玉门关和阳关,军营A、玉门关m和阳关n三地位置如图所示.为了方便传递消息,不延误战机,现需在军营、玉门关和阳关三地之间建立通道,传令兵从军营出发,依次将消息传给玉门关和阳关后回到军营.请问玉门关和阳关在哪建立哨所能使传令兵所走路径最短?
思路引导:利用轴对称,化折为直.
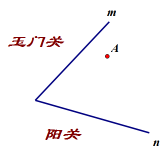
【设计意图】侧重于巩固所学知识,并在探究两条线段和的最短问题的基础上进一步探究三条线段和的最短问题。通过知识迁移,让学生利用轴对称知识进一步巩固解决最短路径问题的基本策略和基本方法。设计时注意了问题的广度、深度和梯度。
通过今天的学习,你有什么收获?你有什么感悟?
将军饮马问题
条件特点:“两定一动”、“一定两动”
问题特点:求线段和的最小值
求解思路:利用轴对称,化折为直
求解原理:两点之间,线段最短.(或“三角形任意两边之和大于第三边”)
(一)基础演练
1.如图,在 中,
中, ,
, 是
是 的两条中线,
的两条中线, 是
是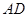 上一个动点,则下列线段的长度等于
上一个动点,则下列线段的长度等于 最小值的是( )
最小值的是( )
A. B.
B.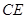 C.
C.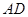 D.
D.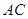

2.在第1题的条件下,若 为等边三角形,
为等边三角形,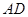 =3,求
=3,求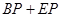 的最小值.
的最小值.
(二)变式提高
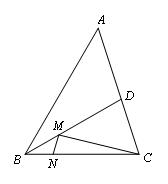
3.如图,在锐角三角形ABC中, 面积为6,AB=4, BD平分∠ABC,交AC于点D,M、N分别是BD,BC上的动点,求CM+MN的最小值.
面积为6,AB=4, BD平分∠ABC,交AC于点D,M、N分别是BD,BC上的动点,求CM+MN的最小值.
4.将军准备从军营A出发,外出前往玉门关m和阳关n视察军情,然后再去粮草藏匿地B查看,最后再回军营.已知军营A、粮草藏匿地B、玉门关m和阳关n四地位置如图所示.请问将军怎么走,路径最短?

(三)拓展延伸(选做题)
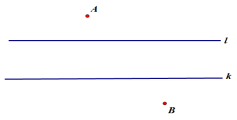
5. 战事临近,将军将要出兵,已知军营A和战场B分列于河流的两岸(河流的两岸是两条平行的直线l,k),由于河流很宽,需要架桥才能通过,为了桥的稳固和安全,桥面需垂直于河流两岸,请问将军在哪里架桥,行军路径最短?
【设计意图】综合应用,能力提升;分层布置,有效巩固;拓展延伸,开拓思维.
设为正确答案